【ソートアルゴリズムとは？】選択ソート・マージソートについて解説

はじめに

今回のテーマは、ソートアルゴリズムの選択ソートとマージソートに触れていきます。
自分は、ソートアルゴリズムを勉強し始めた頃、種類が多く感じ、もう苦手意識が生まれていました…。(なにかの呪文を並べられているような…)
でも実際に勉強してみると、それぞれのソート方法が持つ動きが独特で、おもしろくも感じ始めました。

口下手であまり説明が得意ではない自分ですが、なるべく簡潔に、着眼点をしっかり押さえられるような説明を意識して書いていきますので、ぜひ最後までお付き合いいただければと思います。

アルゴリズムについて学習中の方は以下の記事も合わせてご覧ください！

ソートアルゴリズムとは

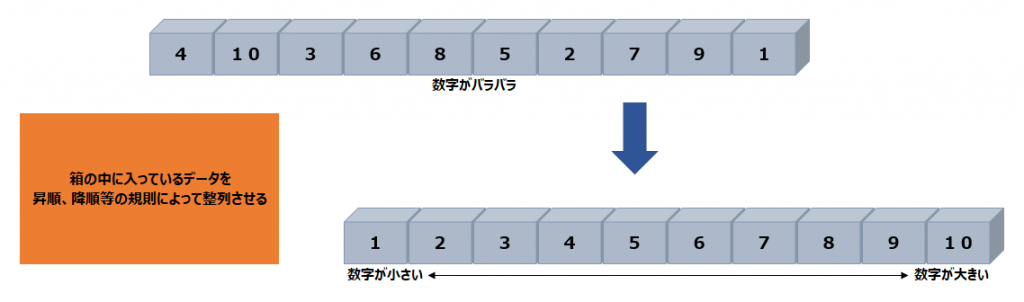
データの集合を大小関係などの規則性によって整列をさせるアルゴリズムをソートアルゴリズムと呼びます。
データベースを始め、プログラミングでは大量のデータを扱うことが多くなるため、データを昇順や降順等、データベースに格納されたデータを一定の規則に従って整列させる必要があり、その際にソートアルゴリズムの知識や技術は、非常に重要ものになります。

ソートアルゴリズムの種類

ソートアルゴリズムには様々な種類があり、整列方法や計算量などが異なります。そのため、実際の業務バランスを見て効率の良いものを選ぶ必要があります。
代表的なもので言うと、バブルソート、選択ソート、挿入ソート、マージソート、シェルソート、クイックソート、ヒープソート、etc…
たくさんありますね…。その中で今回は、表題の選択ソートとマージソートに絞ってご紹介をしていきます。

選択ソート(基本選択法)

選択ソートとは

対象データ列から最小値もしくは最大値を選択し、交換を繰り返す整列方法を選択ソートと呼びます。未整列の要素の中から最大もしくは最小のものを選択し、整列済みの列の末尾に追加していくものになります。

選択ソートの例

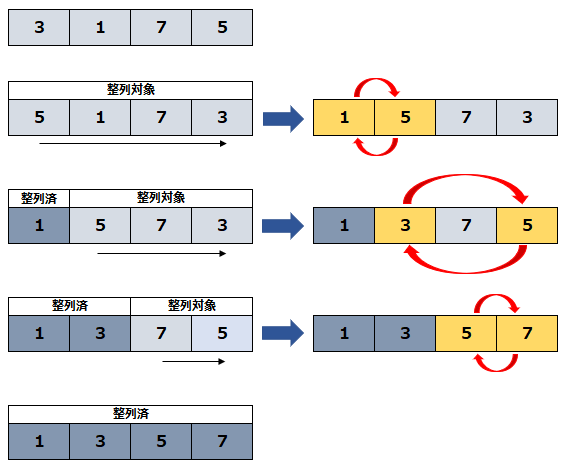
「3,1,7,3」と並んでいるデータを昇順に並べ替えます。

まず整列対象の中から最小値を探す。最小値が「1」のため、先頭データと入れ替える。「1」は整列済みとする。
残りの整列対象の中から最小値を探す。最小値が「3」のため、先頭データと入れ替える。「1,3」は整列済みとする。
残りの整列対象の中から最小値を探す。最小値が「5」のため、先頭データと入れ替える。「1,3,5」は整列済みとする。
残りの整列対象が「7」のみのため、全てのデータが整列済みとし、終了。

このいった動きをする方法が選択ソートとなります。
重要なのは、未整列のデータの中から最小値を見つけて交換していく、これを繰り返すことで整列が完了するということです。

計算量

計算量はO(n²)のため、処理速度は低速です。

マージソート(併合整列法)

マージソートとは

再帰を利用したアルゴリズムで、対象データ列を再帰的に分割したうえで、再び併合を繰り返していく整列方法をマージソートと呼びます。

マージソートの例

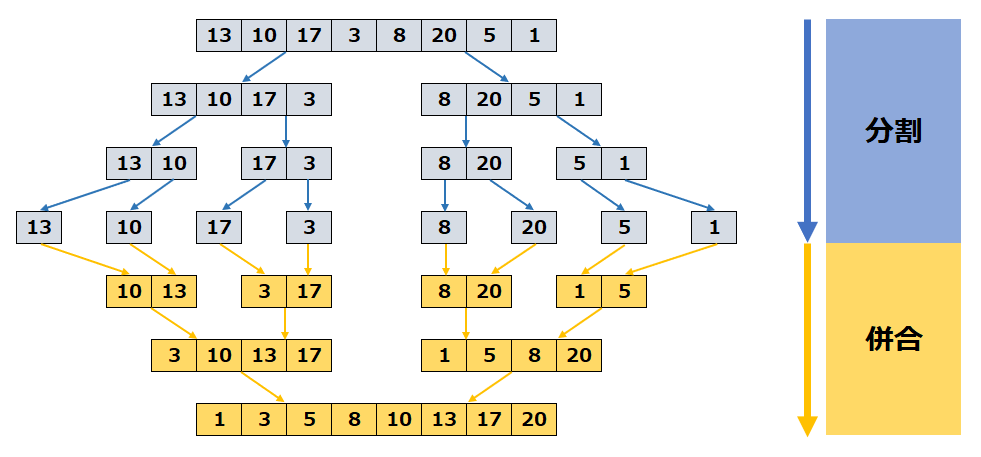
「13,10,17,3,8,20,5,1」と並んでいるデータを昇順に並べ替えます。

まず整列対象データ「13,10,17,3,8,20,5,1」を「13,10,17,3」と「8,20,5,1」に分割する。
「13,10,17,3」を「13,10」と「17,3」に分割、「8,20,5,1」を「8,20」と「5,1」に分割する。
「13,10」を「13」と「10」に分割、「17,3」を「17」と「3」に分割、「8,20」を「8」と「20」に分割、「5,1」を「5」と「1」に分割する。
「13」と「10」を小さい順の「10,13」として併合、「17」と「3」を小さい順の「3,17」として併合、「8」と「20」を小さい順の「8,20」として併合、「5」と「1」を小さい順の「1,5」として併合する。
「10,13」と「3,17」を小さい順の「3,10,13,17」として併合、「8,20」と「1,5」を小さい順の「1,5,8,20」として併合する。
「3,10,13,17」と「1,5,8,20」を小さい順の「1,3,5,8,10,13,17,20」として併合し、終了。

こういった動きをする方法がマージソートとなります。
併合する際は、2つの列の先頭のデータを比較し、小さいもしくは大きい方を取り除いて併合列に追加する、2つの列の内部はすでに整列済みであるため、両方の列のデータがなくなるまで、これを繰り返すことで整列が完了するということです。

計算量

平均計算量・最悪計算量ともにO(n log n)のため、安定した高速で動作します。ただし2つのデータを併合する際、外部領域を必要とします。
最後の併合n/2個のデータを保持できる領域が必要になり、つまりメモリ使用量にO(n)を必要となります。

さいごに

今回ご紹介させていただいたソートアルゴリズムは、選択ソートとマージソートのみとなりました。
選択ソートについては、仕組みは簡単で分かりやすい整列方法なのですが、1つずつ最小値もしくは最大値を確認しているため、膨大なデータを整列させる際は、大分手を焼きます。
対してマージソートは、平均計算時間も最悪計算時間もO(n log n)となり、極めて高速な整列方法ですが、元のデータ列と別に作業用の記憶領域を必要となります。
各整列方法は、時と場合により、それぞれ向き不向きが出てきてしまうため、実際の業務バランスを見て判断するというのも大事なことなのです。

以上、お付き合いいただきありがとうございました。